Visa en fördelning per maskin
Visa gemensam fördelning

![]()
![]()
![]()
Data för SPC och statistik, Nolato AB
Denna sida innehåller exempel och övningar på histogram, fördelningar, duglighet, etc.
Info, referenser, m.m...
Antal mätvärden per maskin:
Totalmedelvärde:
Medelavvikelse maskin 1:
Medelavvikelse maskin 2:
Medelavvikelse maskin 3:
Medelavvikelse plasttyp 11:
Medelavvikelse plasttyp 12:
Standardavvikelse:
Undre toleransgräns:
övre toleransgräns:
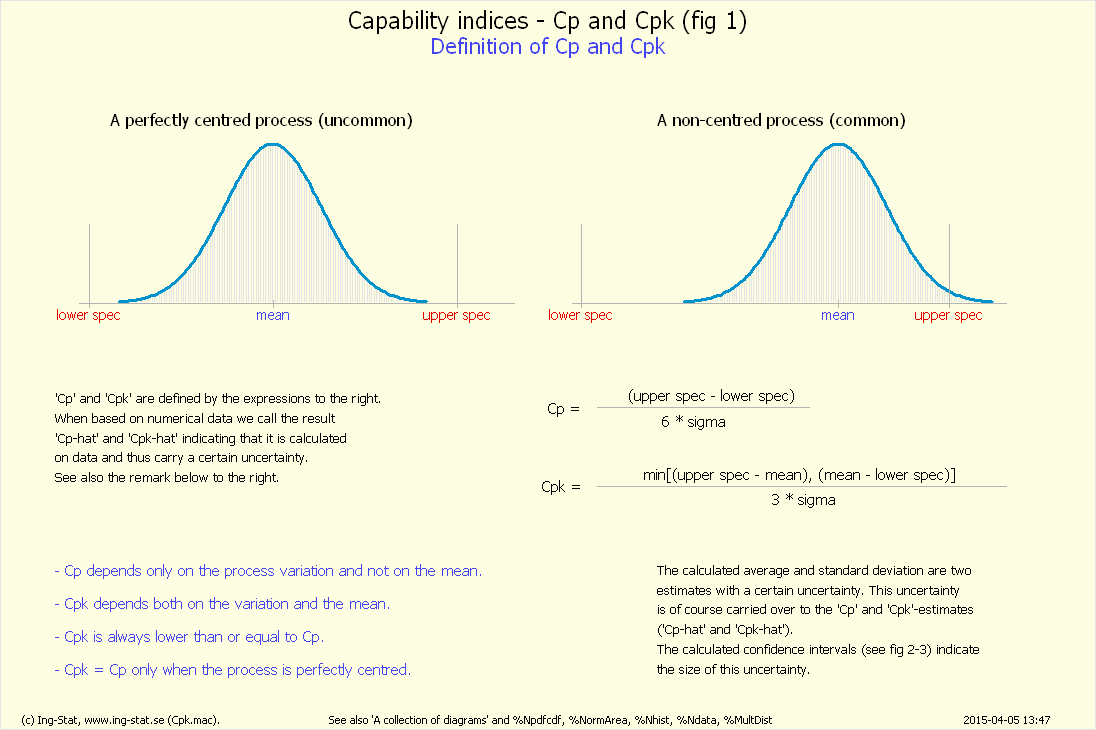
%Cpk (fig 1)...
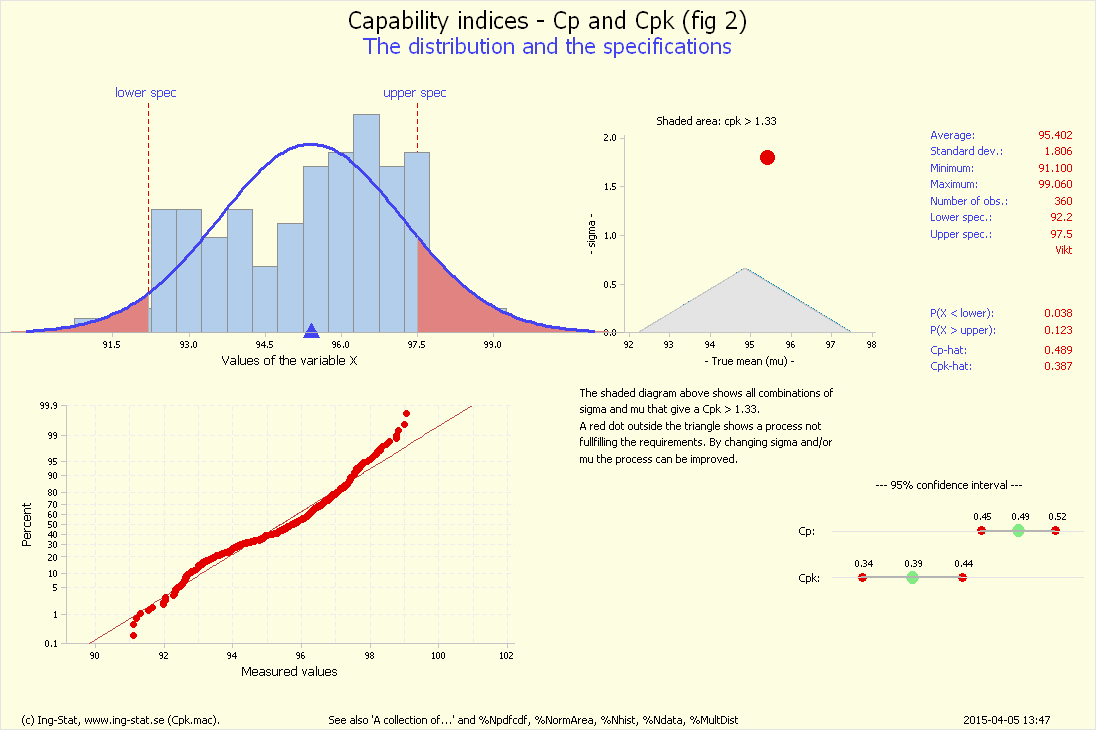
%Cpk (fig 2)...
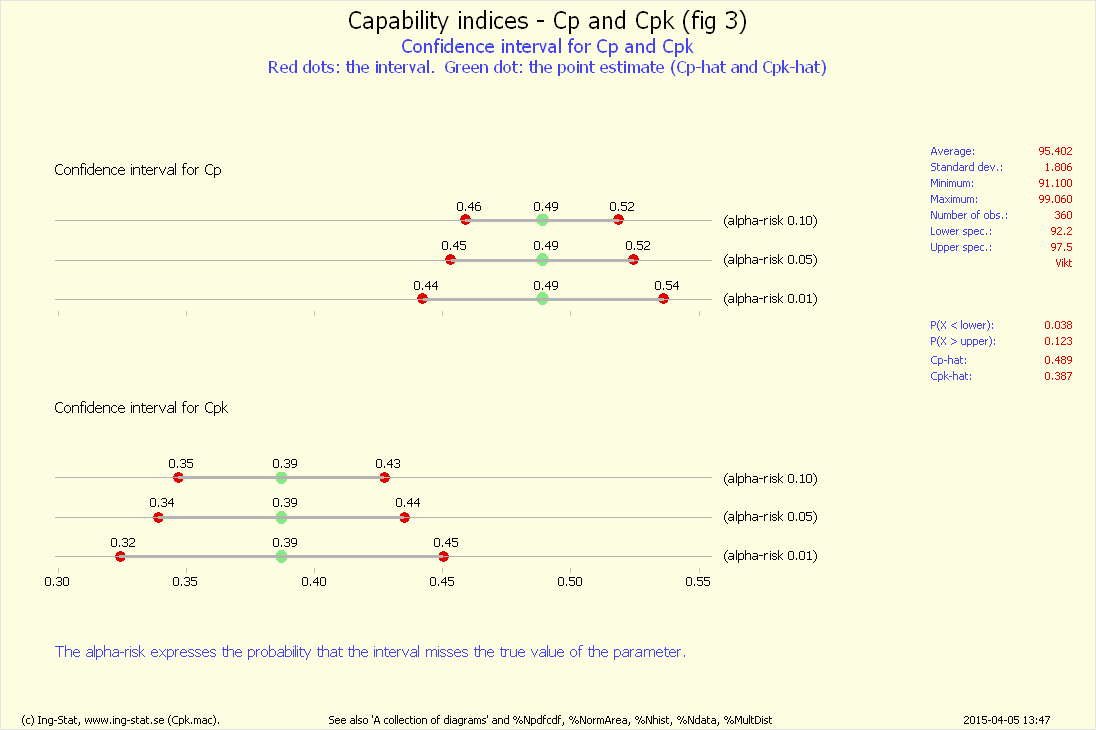
%Cpk (fig 3)...
![]()
Varje ruta innehåller parametervärden som används för att simulera data för analys (data skapas med makrot %Nolato). En ändring registreras direkt i rutorna till höger:
Antal mätvärden per maskin: I denna övning finns det tre maskiner (1, 2, 3) och antal simulerade mätvärden per maskin skrivs in i rutan.
Totalmedelvärde: Här anges totalmedelvärdet, ett medelvärde som är beräknat över samtliga mätvärden.
Medelavvikelse maskin 1: Om resultatet för maskin 1 är annorlunda (högre eller lägre) anges det här som medelavvikelse från totalmedelvärdet.
Medelavvikelse maskin 2: Se kommentar för 'Medelavvikelse maskin 1' ovan.
Medelavvikelse maskin 3: Eftersom totalmedelvärdet och medelavvikelserna för maskin 1 och 2 är bestämda, måste medelavvikelsen för maskin 3 beräknas.
Medelavvikelse plasttyp 11: I denna simulering finns det två plasttyper (11, 12) och 1/3 av alla data är från plasttyp 11. I rutan anges här medelavvikelse för plasttyp 11.
Medelavvikelse plasttyp 12: Eftersom totalmedelvärdet och medelavvikelserna för plastyp 11 är bestämda, måste medelavvikelsen för plasttyp 12 beräknas.
Standardavvikelse: I verkliga datamängder finns det en variation. Här simuleras detta med en slumpkomponent som adderas till mätvärdena ovan. (Slumpkomponenten är normalfördelad med medelvärde 0 och standardavvikelse enligt rutan.)
Undre toleransgräns: Här anges processens undre toleransgräns.
övre toleransgräns: Här anges processens övre toleransgräns.
Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att skapa data
i Minitab måste raden '%Nolato...' manuellt kopieras in i Minitab och aktiveras. Därefter kan analysen utföras.
Det finns tre knappar som visar övningar och texter (övningar i pdf-format kan skrivas ut och användas). De tre blå länkarna visar
exempel på grafer som skapas av %Cpk-makrot i Minitab.
••••
Rutan visar tre fördelningar: blå är 'maskin 1', röd är 'maskin 2' och grön är 'maskin 3'.
(Om det syns bara en eller två fördelningar innebär det att två eller fler maskiner har samma medelavvikelse.)
De tre vertikal linjerna motsvarar de två specifikationsgränserna (röda) samt processens medelvärde (grå).
Varje fördelning är en blandning av två plasttyper och om dessa har tillräckligt olika medelavvikelser, blir
fördelningarna icke-symmetriska eller – om medelskillnaden är ännu större – tvåtoppiga.
Om markören förs över graffönstret visas en vertikal blå linje. Det ena värdet
är linjens läge på X-axeln, det andra värdet är avståndet i procent till de två toleransgränserna.
Klicka på den blå linjen för att lagra ett nytt totalmedelvärde för processen.
Med de två radioknapparna ovan fördelningarna är det möjligt att visa den totala
fördelningen. Denna motsvarar det histogram som visas i Minitab då nedanstående kommandon har körts.
Observera 1/3 av alla mätningar gäller 'plasttyp 11' och 2/3 gäller 'plasttyp 12' (detta är inprogrammerat).
De två plasttyperna är slumpmässigt fördelade över de tre maskinerna.
••••
'Kopiera/Klistra in' raderna i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.
Första två raderna simulerar data för den angivna övningen. Övriga rader är förslag på analys och grafer.
Om värdet ändras i någon av indatarutorna visas ett antal radioknappar som skriver in motsvarande kommandon i rutan.
••••
De tre sifferuppgifterna visar det teoretiska medelvärdet och den teoretiska standardavvikelsen (sigma) samt 'Cpk'-värdet på det resultat
som når kunden då processen har nuvarande prestanda.
När t.ex. skillnader mellan maskiner och skillnad mellan plastmaterial
minskas, minskar också spridningen (sigma) och 'Cpk'-värdet ökar på resultat som når kunden.
Indatarutan 'Standardavvikelse:' är spridningen som åtstadkoms av andra variationskällor (dvs inte den variation som kommer av skillnader mellan maskiner eller plastmaterial).
Klicka på radioknappen "Visa gemensam fördelning" (över grafen) för att se fördelningen av resultat som når kunden. (Alla uppgifter kan jämföras med grafen 'fig 2' som skapas efter Minitab-körningen.)
••••
Two expressions for p
The two buttons (logit (p)) and (p) show the same model expressed differently. By rearranging and manipulating
the p-version the logit-version is obtained. The main benefit is that the right side of the equal sign is now a linear expression.
Such expressions are generally much easier to analyze.
The drawback is that the parameters (the betas) are more difficult to interprete
when evaluating the final model.
When a variable is omitted in the model, a red cross covers the variable. (Only in the logit-version.)
••••
Övning 1 – en första körning
Överför kommandona till Minitab-fönstret och tryck [Enter]. Grafen märkt 'fig 2' sammanfattar mätningarna. Totalmedelvärdet är ungefär 95.4 och standardavvikelsen
är ungefär 1.8, Cpk är ungefär 0.39. Processen är alltså inte duglig enligt vanlig standard. Kör 'övning 2'.
Övning 2 – ingen skillnad mellan maskiner
I denna körning finns det ingen skillnad mellan maskinerna. I 'fig 2' visas att medelvärdet är fortfarande ungefär 95.4 och standardavvikelsen har minskat till
ungefär 1.0 och Cpk har ökat till ungefär 0.74. Processen är fortfarande inte duglig. Kör 'övning 3'.
Övning 3 – ingen skillnad mellan plaster
I denna körning finns det heller ingen skillnad mellan plaster. I 'fig 2' visas att medelvärdet är fortfarande ungefär 95.4 och standardavvikelsen har minskat till
ungefär 0.9 och Cpk har ökat till ungefär 0.78. Processen är fortfarande inte duglig. Kör 'övning 4'.
Övning 4 – förändring av medelvärde, standardavvikelse eller specifikationer
Denna körning utgår ifrån 'övning 3'. Gör en körning i Minitab och avgör i 'fig 2' hur man kan förändra medelvärde eller standardavvikelse eller
processens specifikation så att processen får ett Cpk > 1.33. ändra sedan i rutorna och gör en ny körning. Det kan behövas flera körningar.
(Tips: högerklicka triangeln och använd 'Crosshairs' för lättare att avgöra var den röda punkten ligger.)
Övning 5 – 'Probability plots' över maskiner
I denna övning finns det bara skillnader mellan maskinerna, ingen materialskillnad. En 'probability plot' visar tre parallella linjer, något förskjutna.
Det betyder att de tre maskinerna har ungefär samma standardavvikelse (spridning) men olika medelvärden. Resultatet ges också som siffror i en tabell.
Övning 6 – Histogram över maskiner
I denna övning finns det bara skillnader mellan maskinerna, ingen materialskillnad. En graf visar tre histogram, något förskjutna.
Resultatet ges också som siffror i en tabell.
Övning 7 – Ett matrisdiagram
I denna övning ritas ett s.k. matrisdiagram över data. Då man har många kolumner ger ett matrisdiagram en snabb överblick. Analysen
underlättas om man använder s.k. 'brushing' (högerklicka diagrammet).
Övning 8 – Ingen skillnad mellan maskiner, minskad spridning
Ändra manuellt i rutorna så att alla avvikelser för maskin 1, 2 och 3 blir 0. Minska standardavvikelsen till 0.6. Notera att fördelningen passar ganska väl inom
toleransgränserna men att den systematiska skillnaden mellan plastmaterialen framträder. Det finns alltså utrymme för ytterligare kvalitetsförbättringar genom
att undersöka och eliminera skillnader mellan materialen.
Övning 9 – Ingen skillnad mellan maskiner eller material, Cp = Cpk = 1
Ändra manuellt i rutorna så att alla avvikelser för maskiner och plasttyper blir 0. Skapa en centrerad process och välj en standardavvikelse så att det blir exakt
6 standardavvikelser mellan undre och övre specifikationsgräns. Notera att fördelningen passar precis inom specifikationsgränserna.
Kör %Cpk i Minitab och notera att Cp och Cpk blir nära 1.
Övning 10 – Ingen skillnad mellan maskiner eller material, Cp = Cpk = 1.33
Ändra manuellt i rutorna så att alla avvikelser för maskiner och plasttyper blir 0. Skapa en centrerad process och välj en standardavvikelse så att det blir exakt
8 standardavvikelser mellan undre och övre specifikationsgräns. Notera att fördelningen passar väl inom specifikationsgränserna.
Kör %Cpk i Minitab och notera att Cp och Cpk blir nära 1.33.
••••
Länkar
Confidence interval for p (ENG)
The animation shows how a confience interval for p should be intepreted. Here p
('proportion', 'fault rate', etc) is the unknown parameter to be estimated
from a dataset.
Several distributions with common μ and σ (ENG)
The animation shows several distributions with common μ and σ. By two slides these values can be changed
and the corresponding functions visualised.
Simulering av kapabilitetsindex Cpk
Ett kapabilitetsindex är ett index som försöker sammanfatta förhållandet mellan utfallet
från en process och dess specifikationer.
A mixture of distributions (ENG)
An animation that shows what happens when distributions are mixed.
Simulating a comparison of two proportions (ENG)
A simulation that shows some of the difficulties when comparing two proportions.
Animering av en enkel OC-kurva
Här animeras en enkel OC-kurva som beskriver vissa egenskaper hos ett enkel stickprovsförfarande.
Simulering av talet pi — Buffons nål
Här simuleras och animeras Buffons nål — ett klassiskt sätt att simulera det berömda talet pi.
Konfidensintervall
Här simuleras och animeras flera grundläggande egenskaper hos ett konfidensintervall.
Ett antal fördelningar
Initialt visas en Weibullfördelning men ett antal kontinuerliga och diskreta fördelningar kan visas via en länk. För varje fördelning kan parametrarna ändras
steglöst så att fördelningarnas form och läge uppdateras.
Avverkning av felrapporter
Simuleringen visar hur antal felrapporter minskar då antal 'ut' överstiger antal 'ut' och minskningen sker ungefär som en rät linje.
Variationen vid RTL ("Ready To Launch") påverkas kraftigt då 'utintensiteten' förändras.
Kvalitetsbristkostnader
Simulering av en enkel process (utan alternativa flöden) där en enhet kan ha upp till fem olika fel. Det finns tre teststationer där
felen kan upptäckas eller passera oupptäckta (den sista teststationen är kunden).
En Markovkedja
Simulering av en enkel s.k. Markovkedja. En sådan beskrivs ofta som en process med flera steg och där ett 'ärende' kan hoppa omkring med kanske
inget eller flera slut. En hiss kan ju gå från olika våningar men kommer aldrig fram medan ett bankärende eller felrapport kommer att avslutas förr eller
senare.
En Quincunx
En s.k. Quincunx är en enkel apparat där man låter kulor e.d. falla ned mot någon typ av stopp och på så sätt visa hur summan av
en mängd små händelser leder till ett normalfördelat utfall.
Minitab-makron
%2000 Makrot plottar 2000 punkter (som tidigare simulerats) och diagrammet visar en kanske oväntad form men helt i linje med statistisk teori. Kräver en viss kunskap om binomialfördelningen.Några dokument
Några erfarenheter
Några erfarenheter med att arbeta med data.
Ett antal dokument
Mer än 25 olika dokument om varierande område inom statistik och statistisk analys. Se t.ex. "What is sigma?" som har en
noggrann genom av vad sigma är, hur sigma skall tolkas, hur sigma kan beräknas, etc.
••••